Configure analysis
The analysis is configured by clicking on Configure Analysis button in the main menu (see details). Note that before starting the computation the data must be read. This button opens the menu that helps to define the analysis. The menu is now shown ready to (a) compute polychoric correlations (with categories from 1 to 5), (b) compute parallel analysis, (c) retain two factors computed by Unweighted Least Squares factor analysis, (d) compute robust factor analysis, and (e) rotate the solution oblique Procuestean Rotation using the user provided target matrix. In addition, the output is stored in file output.txt.
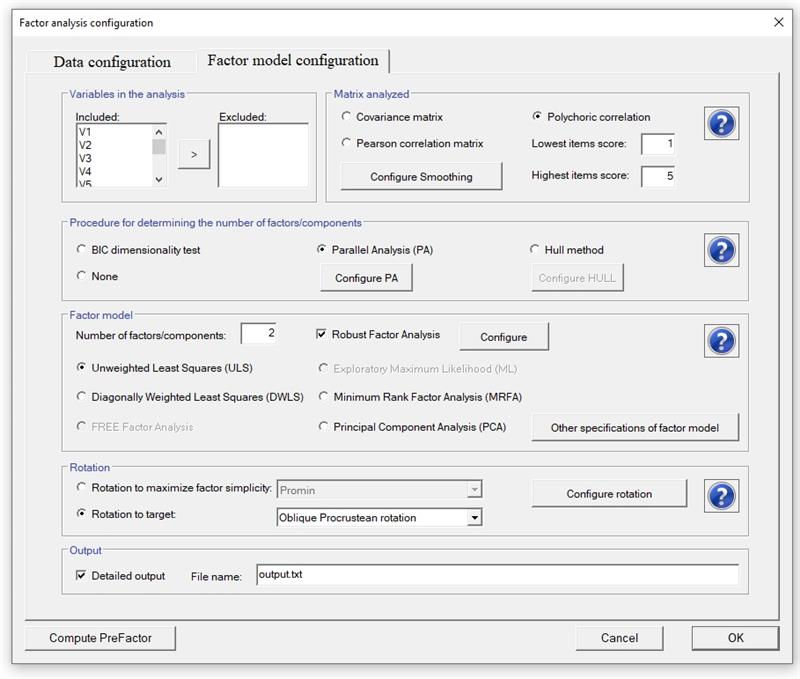
When computing the polychoric correlation, please note that:
- Factor computes the lowest and the highest answer in the data, and takes these values as default values.
- A value lower than the value observed in the data is not allowed.
- All the variables are expected to have the same number of categories of response.
- If the matrix is not positive-definite, a smooth algorithm is computed to solve it.
- If a polychoric correlation coefficient cannot be computed, the corresponding Pearson correlation is computed. If a large number of polychoric correlation coefficients cannot be computed, the analysis will be based only in Pearson correlation matrices.
- If the number of Factors/Components is set to the value of zero, the greatest lower bound (glb) to reliability is computed. The glb was defined by Woodhouse and Jackson (1977), and it is computed according to the algorithm suggested by Ten Berge, Snijders and Zegers (1981) as a modification of Bentler and Woodwards method (1980). This lower bound is better than coefficient alpha, but can only be trusted in large samples, preferably 1000 cases or more, due to a positive sampling bias.
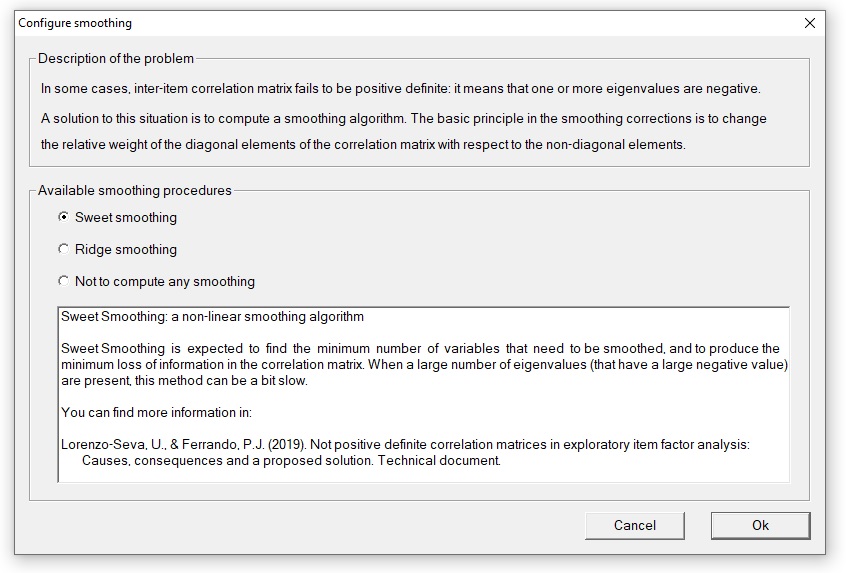
Least-squares exploratory factor analysis based on tetrachoric/polychoric correlations is a robust, defensible and widely used approach for performing item analysis. A relatively common problem in this scenario, however, is that the inter-item correlation matrix might fail to be positive definite. In order to correct not positive definite correlation matrices, FACTOR implements smoothing methods. The basic principle in the smoothing corrections is to change the relative weight of the diagonal elements of the correlation matrix with respect to the non-diagonal elements. The challenge of the smoothing methods is to change the relative weight of the diagonal elements of the correlation matrix while destroying as little variance as possible in the process. In the present release of FACTOR, Ridge and Sweet smoothing methods have been implemented. It must be noted that Ridge Smoothing is a linear smoothing method that impacts all the variables in the correlation matrix. To prevent this from happening, we propose Sweet Smoothing: the aim of this non-linear smoothing method is to focus the smoothing procedure only on the problematic variables while destroying as little variance as possible in the process. The researcher is allowed to choose between these two smoothing methods when analyzing a dataset.
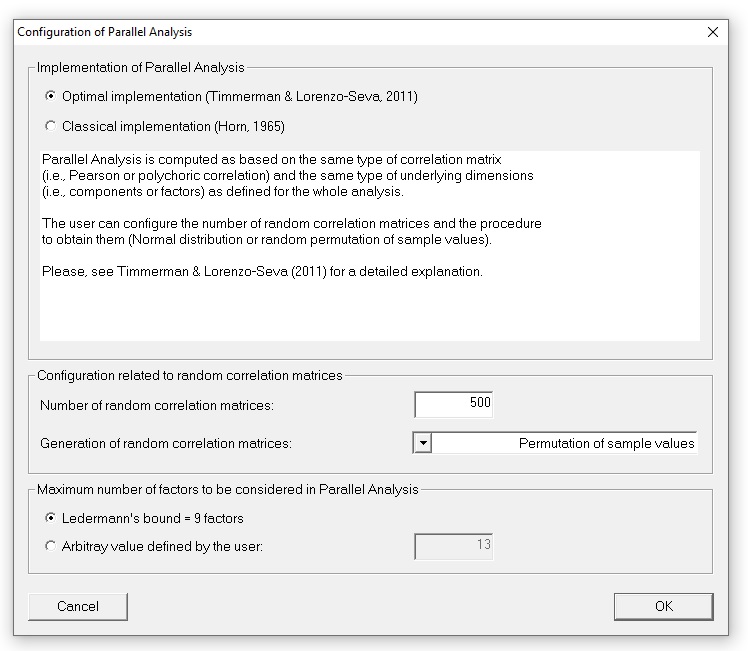
Different implementation of PA can be computed. This menu describes how PA can be configure:
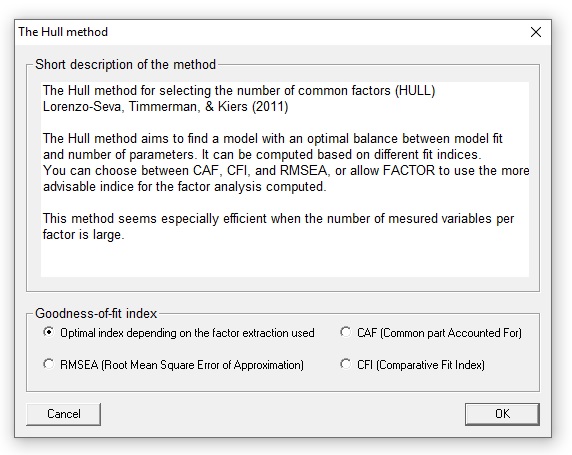
Hull method is a procedure to assess the number of factors to retain. This menu describes how Hull method can be configure:
When robust factor analysis is selected (and bootstrap sampling has been allowed when reading the dataset from disk), the user can configure the different aspects shown in this menu:

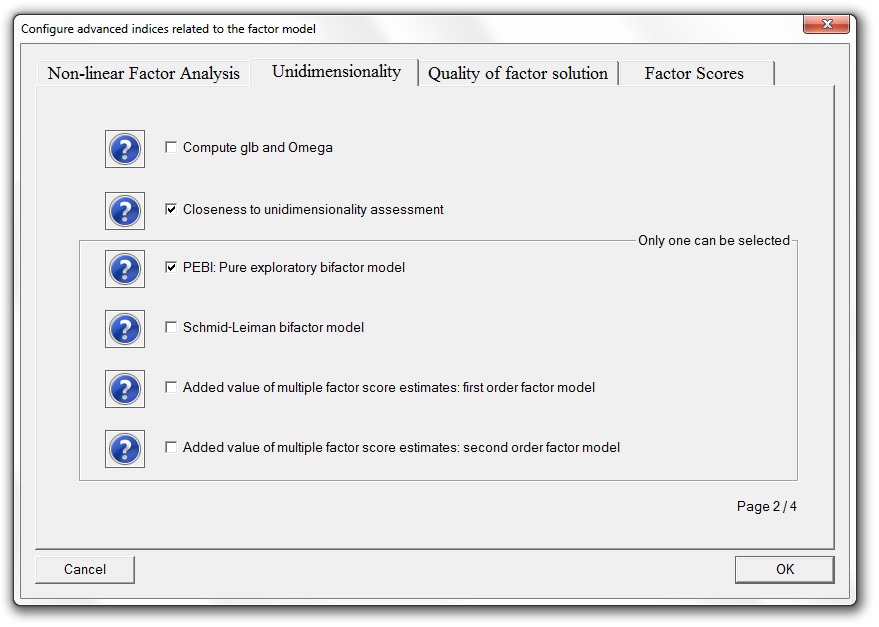
Advanced specifications of the model can be configured using this menu, that is shown ready to (a) display IRT parameterization; (b) compute factor scores and related indices and procedures (like DIANA); (c) compute continuous person-fit indices; (d) compute bifactor model (PEBI); and (e) to compute different indices related to essential unidimensionality and the quality of the factor solutions:
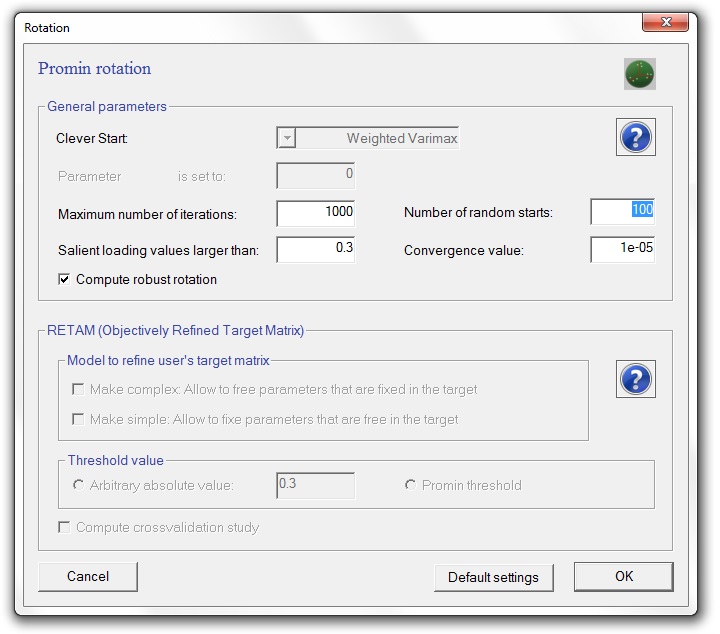
We implemented many methods to obtain simple structure. To configure the parameter values, the Configure rotation button opens the following menu:
This menu shows the default parameter values of Normalized Direct Oblimin. These values are:
- Clever start: This is a pre-rotation method computed as a starting point for the Oblimin rotation.
- Parameter gamma set to: This defines a default value for the parameter gamma of Oblimin.
- Number of random starts: To avoid convergence to local maxima, each rotation is computed from a number of random starts, and the rotated solution that attains the highest criterion value is taken as the solution for the analysis.
- Maximum number of iterations: This defines the maximum number of iterations in the rotation method.
- Convergence value: This defines the convergence value to finish the rotation method.
- Salient loading values larger than: This defines the minimum value of the salient loadings to be printed in the cleaned loading matrix. If the value is set to zero, the cleaned loading matrix is not printed.
When a Target matrix is provided, the target can be refined using Objectively Refined Target Matrix (RETAM). When a target matrix is proposed by the user, RETAM helps to refine the target matrix allowing to free and to fixe elements of the target matrix. RETAM risks to capitalize a factor solution on chance (i.e., the factor model is fitted to the sample at hand, not to the population). In the RETAM crossvalidation study, the sample has been half-splitted in two random subsamples: RETAM procedure is applied in the first subsample in order to obtain a refined target matrix; and the refined target matrix is then taken as a fixed target matrix (without further refinements) for the second subsample. If the rotated loading matrix in the second subsample is congruent with the rotated loading matrix in the first subsample, then the researcher must be confident that the final solution has not just been fitted to the sample data, but also to the population data. Here you have an example how to configure it:
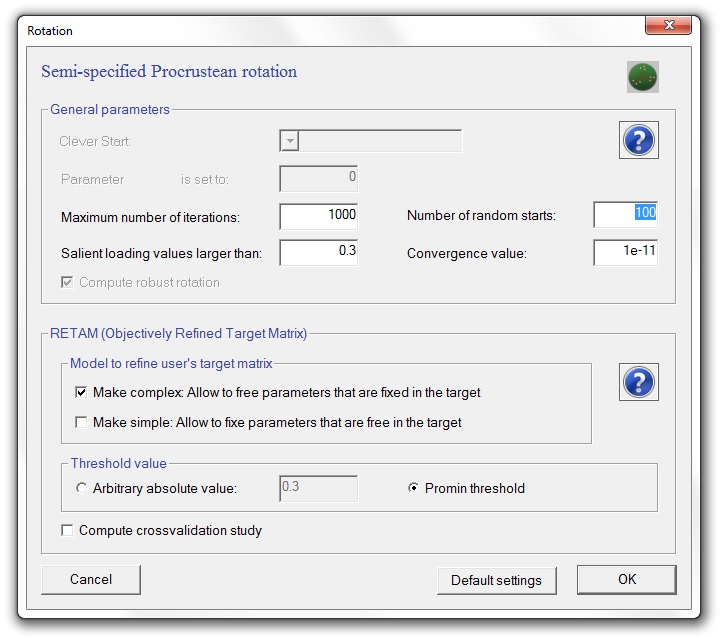
The default button sets the parameters of the rotation to the usual values in the literature. These values are the ones defined when the program starts.
When simplimax rotation is used, a range of salient loading values (and a final number) must be specified. This is done during the computation itself (see details).
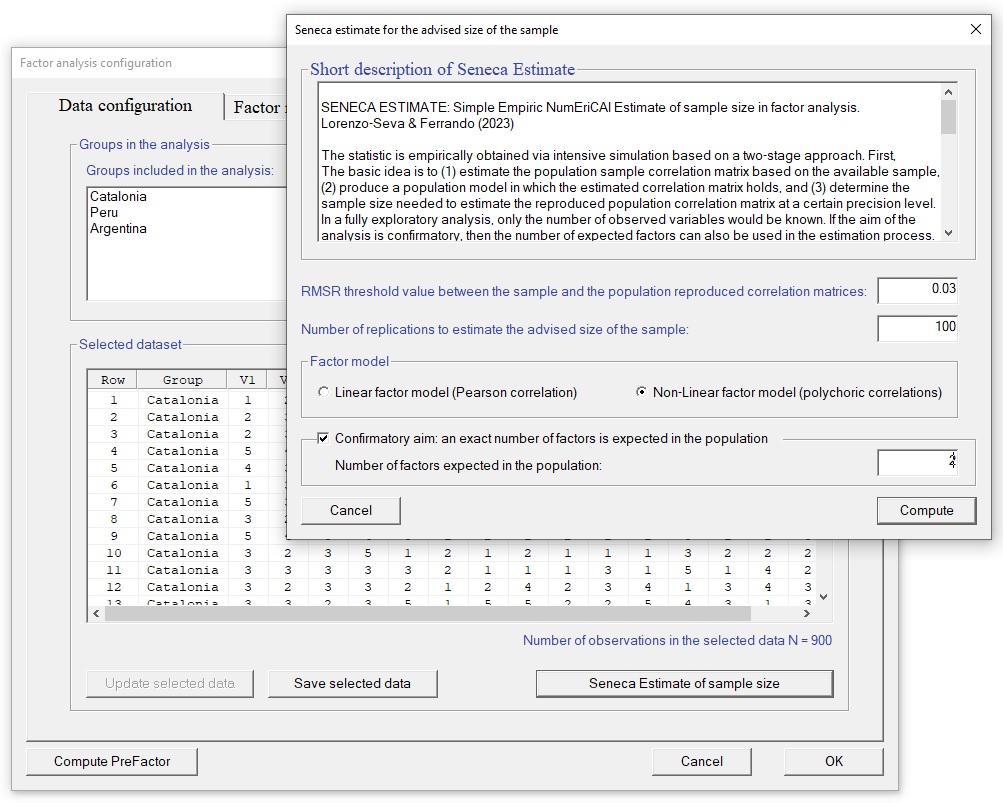
Seneca Estimate is a procedure to estimate an optimal sample size. The proposal is based on an intensive simulation process in which the sample correlation matrix is used as a basis for generating datasets from a pseudo-population in which the parent correlation holds exactly. And the criterion for determining the needed size is a threshold that quantifies the closeness between the pseudo-population and the sample reproduced correlation matrices.